2.6.1 Axioms Part 1: Overview

A Definition of Axioms
A useful and reasonably standard dictionary definition of ‘axiom’ reads:
“A statement or proposition which is regarded as being established, accepted, or self-evidently true” (source).
Notice that this definition does not invoke logic. Perhaps more to the point, it does not imply that ‘definition’ is a characteristic of axioms. Indeed the statement quoted above seems to imply that axioms are true because they are true. By this way of thinking, we merely make a declaration (of truth or acceptance) or say that something is the case. Examples of such declarations might be ‘geometric points exist’, ‘atoms exist’, ‘the Sun God exists’. (These are discussed in greater detail below.) Although truth by declaration seems, in some respects, unsatisfactory, especially when applied to the descriptive beliefs systems of science, we will see that axioms are to some extent inescapable.
Pragmatism About Axioms: Does truth have to be a characteristic of axioms?
If we cut the words “self-evidently true” from the last sentence of the dictionary definition, I believe that we can still maintain the overall sense and pragmatic (or epistemic) importance of axioms. The definition would then become,
An axiom is ‘a statement or proposition which is regarded as being established and accepted’.
This construction does not prevent us from thinking that the more firmly we believe (axiomatic) statements, the more likely we are to regard them as explanatorily valuable.
If we were scientists, we might want to develop that definition further and say that axioms are ‘established, accepted and possess some explanatory power and must facilitate testable predictions’. If we wanted to emphasise the social and cultural aspects of belief systems the definition might then become ‘an axiom is an important statement that is socially well established and fits within a framework of belief used in a particular historical period’. This perspective on axioms accommodates the historical rise of science and other academic disciplines. The historicised view also helps us to understand that amongst the community of physicists, for example, individuals come to invoke new ideas over time based on a change of the axioms.
Outline and Scope
In this essay, I argue that axioms should be seen as fundamental assumptions bound by context rather than unchangeable truths.
The first purpose of this essay is to demonstrate that sets of related axioms play an important role in various kinds of analytical and descriptive systems. I take the view that axioms should not be regarded as absolute or immutable statements that proclaim idealised truths. (Indeed, that is for me a pragmatic axiom about axioms.) For me, they are temporarily important assumptions needed to develop evolving systems of belief. So that the discussion is not too abstract I have tried to illustrate my argument with respect to logic, mathematics, chemistry biology and physics and religion. Since it is difficult to find composite sources I have created long lists of informal statements to illustrate the enormous diversity of ideas which axioms can encompass. (Only read these lists if they are of particular interest to you.) I try to demonstrate that sets of axioms declare the existence of things and their properties. Lastly, I argue that axioms are important ideas within internally coherent areas of thought and have a social importance in groups of believers.
Sets of Axioms
When we consider that sets of axioms can act together to form the basis of a domain of thought their importance becomes more obvious. By convention, each axiom within a set needs to be independent of the others. Philosophers and mathematicians generally take the view that in an ideal belief system, the set of axioms is complete, none of the individual axioms are redundant, and there is no contradiction. Redundancy means that a candidate axiom can be derived from others within the set. Since sets of axioms can be modified (as described below), it is perhaps better to think of these sets of statements as the most basic assumptions we make when constructing beliefs systems rather than view them as idealised truths.
Types of Axiomatic Sets
Although there are, in practice, an unlimited number of axioms that we could form, it is convenient to think of them as falling into categories. For very good reasons, axioms are often thought of as either logical or non-logical. As a matter of convenience for the following discussion, I will use 3 major categories, which we can call logical, mathematical, and descriptive.
- Descriptive axioms are idealisations of our most basic assumptions about what there is in the world and their properties. They are to some extent equivalent to the premises of an argument.
- Logical axioms are concerned only with the basis on which entities (or ideas) are conceptually related. We can, therefore, use non-meaningful placeholders for those entities to express ideas that are centred on the meaning of logical connectives and modalities (as described in the previous sub-section of this work).
- Mathematical (and descriptive) axioms need to include declarations concerning the existence of something such as a number, a sequence, a set, a point, a line and so on, and some functions or operators. Any well-formed mathematical theorem or proof should in principle have a logically definable basis since mathematics does not extend beyond tautology. Mathematical axioms can, therefore, be categorised as logical.
Often belief systems develop before they are axiomatised. In other words, we develop a series of interrelated ideas then ask what are our most basic assumptions about those ideas.
Axioms and Network Theory
From my point of view, we need not see axioms as foundational in the traditional sense even if they relate to fundamental entities. When I have said that axiomatic or core beliefs are assumptions that act as the basis for a domain of thought I do not mean it in the sense that they form a foundation on which other beliefs are built. My alternative view is that from a network or graph theory perspective, they are merely a set of important nodes in a belief domain network with a very high degree of strong interconnection.
I ask you to think of this graphic of a network by Martin Grandjean as a very approximate metaphor for 3 interconnected domains of contemporary thinking. Consider the points (or nodes) of the network to be ideas and the lines as logical connections. Source: https://commons.wikimedia.org/wiki/File:Network_Visualization.png
From my perspective, axiomatic nodes give the appearance of being necessary because their removal would lead to a great disruption of pathways through the conceptual network. This view is alternatively known as a coherentist theory of truth or justification. (I will return to this theme in another essay.) For me, a belief network also extends to groups of people and is propagated diachronically (over time).
The Communal Nature of Axioms
One aspect of belief sharing with others is that we share axioms between individuals and groups of people (such as scientists). As the views of scientists change over time this can involve changes in the axioms, as we have seen above. These alterations of thought then ripple through the various specialist communities, often causing disputes along the way. One interesting current dispute is whether or not the mass extinction of 66 million years ago, at the Cretaceous–Paleogene boundary, was caused by a giant asteroid impact or volcanic activity in India or a mixture of both. One of the problems in resolving such disputes is that there are no axioms that can inform the debate. The situation is far too complex and goes way beyond the gross simplicities and idealisations of present-day physics. Eventually, experimental and observational tests of belief are used so that disputes are, to a large extent, resolved. If a new theoretical framework arises from the making of observations and as a consequence that axioms have to be changed, so be it. There is nothing aberrant about changing our most cherished beliefs to produces more coherent and predictive narratives.
By contrast when we examine the role of axioms (or core beliefs) in less systematic belief-sharing social frameworks such as religious groupings on a historical time-scale, the transmission of core beliefs (or dogmas) appears more socially divisive. This is partly due to the difficulty (or even impossibility) of reaching definitive proofs that can be agreed on non-empirically. Despite this situation, socially communicated religious teachings often place a great emphasis on axioms, or core beliefs, and their supposed long-term endurance. Religious adherents cannot easily disparage their shared axioms of thought without either ‘betraying’ their group identity or forming new social groups.
The formation of new religious groupings is well epitomised by the complex history of the Church(es) of Scotland. Within some subsections of the Churches of Scotland, there is a very resolute emphasis on particular core beliefs. In addition, there is a liberating reduction of social hierarchy brought about by the abolition of bishops and prelates. Papal ex-communication is not a disciplinary option for example. This combination of social factors has helped to create an almost perplexing number of schisms when viewed in a longer-term historical perspective.
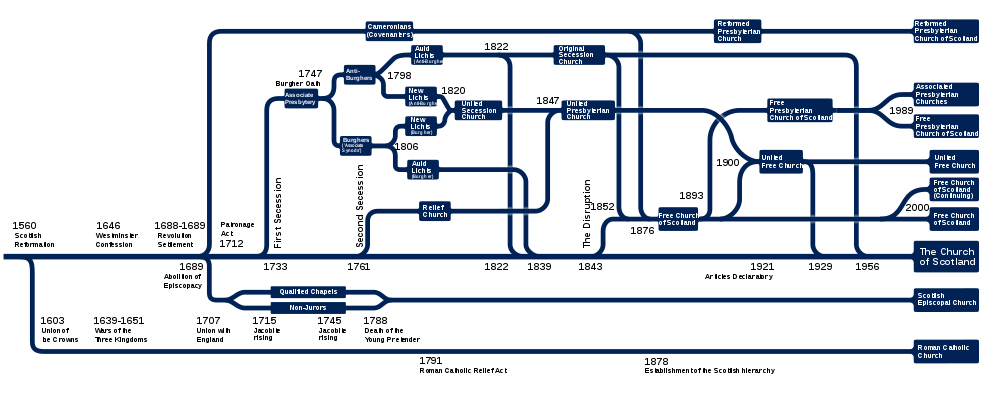
(To see the image above in full detail right-click on it and open in a new tab)
Compare the history of the Roman Catholic Church in Scotland (bottom line above) with that of the Reformed Churches. The existence of social hierarchy that rigidly imposes certain behaviours and axioms of thought on those who claim to be believers has a profound effect on social group identity. By contrast in the reformed, churches varying emphasis on different core beliefs has helped to facilitate the formation of new groupings. Image source Wikipedia: https://commons.wikimedia.org/wiki/File:Reformed_Scots_Church_Denominations.svg created by Hogweard.
Despite the existence of social dynamics and social prominence of certain individuals in scientific communities, there are no papal bulls in science. Even the hard-working and inspired graduate research student can create important new insights that might come to be adopted by the whole community. The pragmatic value of scientific axioms and the role they play in producing more cohesive stories ultimately outweighs any explicit social constraints.
Steve Campbell
Glasgow, Scotland
2017, 2019