2.3 True by Definition

Three ways of thinking about the term ‘definition’ are discussed here:
a) dictionary (or lexical) definitions
b) ostensive definitions (pointing to an example of a thing that is named in a certain way)
c) operational definitions in which a procedure or the description of one is used to create a definition.
Quantitative operational definitions involve the use of a measuring scale of some kind that in itself needs a definition or precise description.
a) Dictionary or Lexical Definitions
It is true to say that a triangle has three sides. However that is merely as a matter of definition. The word we English speakers use to describe ‘a straight-edged three-sided shape’ is not a square; it is a triangle. The word ‘triangle’ is a geometric concept that has a socially agreed meaning for a community of language users and the same word has ended up in standard (or definitive) dictionaries of the English, French and Catalan languages due to the decisions of linguistic communities and their lexicographers. Similar words have ended up in Italian, Spanish, Basque, Corsican, Maltese, Norwegian dictionaries. Progenitor words appear in Latin (Triangulum) and Ancient Greek (trígōnon) . Obviously related words appear in other Indo-European languages such as Polish, Serbian, Gujarati and Hindi for example. We can see from these few selected examples the exact signifier of triangle has evolved and is not fixed in space or in time.
Those who ‘understand’ the current lexical definition can construct and point to triangles which other people (or animals) can acknowledge in some way. In that very restricted sense the definition of a term might be regarded as complete in itself . However as every word included in a definition consists of other words in the lexicon which also require a dictionary entry, no individual lexical definition can have a meaning on its own. It only exist within the frame of reference that we refer to as a natural language. For users of other languages it will make less sense or even be without any meaning. This is why we do not teach very young children by using dictionaries.
There are many different types of triangles that can be conceived and consequently many supplementary definitions that can be arrived at. Often one single word can conjure up extensive possibilities that a simple definition does not seem to capture.
A crude attempt to ‘bend’ the socially acceptable definition of the word ‘triangle’. Potentially there may even be social norms to be modified or challenged in the construction of triangles. Image by Steve.
In forms of creative expression such a poetry or fiction we are often more concerned with richness of emotional and linguistic connotation and to some extent are dependent on this for a desirable vagueness that is rightly unconcerned with operational or logical precision. Without such forms of expression our lives would be impoverished. Definition should not become an overriding preoccupation. Nevertheless in matters of analysis, be they textural, logical or scientific, we must have due regard to what can be achieved by various type of definition.
Normally the definition of a dice might be “a small cube with each side having a different number of spots on it, ranging from one to six, thrown and used in gambling and other games involving chance” (source Google). This definition is based on the notion that there are 6 faces on a cube and dice are always made of cubes. That might be true until some creative person manufactures many 3D shapes that have spots on each face that can be used as dice. In other words definitions should be expected to evolve for cultural reasons.

The standard lexical (or dictionary) definition of ‘dice’ needs revision! Clearly it needs to be made more general. Image by Steve.
Lexical definition is best regarded as facilitator of communication between a community of language users rather than be an absolute standard.
Tautology
It is easier to comprehend an explanation of tautology by example: One definition of ‘parallel’ in geometry is the existence of 2 lines in a flat 2 dimensional plane that never cross no matter how long they extend. This statement is true but is also a tautology in the sense that the property ‘not-crossing’ and being ‘geometrically parallel’ are one and the same.
For the purpose of this discussion, a ‘tautological’ explanation, is a statement in which the interpretation is already implicit in the meanings of the terms used. It has the form ‘p = p’, where ‘p’ is a proposition. A more philosophically precise logical definition of tautology might be: ‘A statement that is true by necessity or by virtue of its logical form’. Dictionary (or lexical) definitions are tautologies and are only true in this sense.
Sometimes truth by definition is referred to as an analytic statement and is distinguished from a synthetic statement that is concerned with something or anything other than definition. This distinction is not particularly helpful, as Willard Quine has argued. Indeed it is the general thrust of the argument laid out here that definition interlocks with many other concepts.
When we wish to define particular words using language, rather than by pointing at something (ostensive definition ), more words are required. These additional words again require definitions and so on in a continuous chain. The linguistic definition as a result does often have the very significant advantage of rich implications and extensive connotations. Indeed this property is partly a direct consequence of the ‘chain of definitions’ that we experience in all forms of analytical thinking. The chain is a boon in ordinary living and in creative activity although a problem for the purposes of rigorous analysis. In short, although we cannot make isolated elemental lexical definitions, we can exploit the power and interrelatedness of definitions as building blocks in making sense of the world and thus be creative and novel in our thinking and actions.
Novel Lexical Definitions
The intellectual construction of a ‘world view’ that we can make through definitions relies on the totality of available linguistic terms. Within a particular natural language we may be faced with the absence of a suitable term, or lexical unit. This is mere accident of cultural history and is referred to as a ‘lexical gap’. If I wish to have a term for a brown or black sheep in order to distinguish them from those that are unpigmented, I simply need to invent a new term such as ‘Sheeb’. We should note however that does not dispense with the word sheep. ‘Sheeb’ would merely be an enlargement of our lexicon.
The same consideration can in principle be applied to other aspects of languages such as logical connectives. If the word ‘if’ is not sufficiently precise we can invent another word, as logicians have already done. They use the word ‘iff’ to mean ‘if and only if’, which has a much more discrete logical implication.
By the invention of new linguistic terms in this way we enrich our ability to define and to create descriptions. In so doing we of course further extend and complicate the logical continuity between description and definition. At times we may be frustrated by lexical gaps and need to adopt a more extended linguistic description or wait for our community of language user to catch up with our latest inventions such as ‘sheeb’.
Although individual sentences can impart meaning ‘Truth by definition’ is not an isolatable property of individual sentences or words. Our language and even our existence are such that individual assertions cannot stand on their own. In principle a dictionary could be finite at any point in the history of a language. However, in a more abstract sense it seems likely that no natural language is likely to be definitionally complete. We can also safely say that no natural language can be comprehensively or completely self-representational or self-definable except by tautology. It is even tempting to believe that at some point or at some higher level of self-representation the ability to form meaningful definitions become vague enough to become meaningless. (Or perhaps this merely reflects my personal difficulties with some philosophical texts.)
b) Ostensive Definition and Its Limitation
Ostensive definitions point to one or more examples of a thing that is named in a certain way. ‘Pointing’ could have a literal meaning in this context or it could refer to a diagram or photograph some other way of drawing a person’s attention to the entity in question. It is the method of choice for teaching very young children an oral vocabulary and so has clear links to the concept of conditioning.
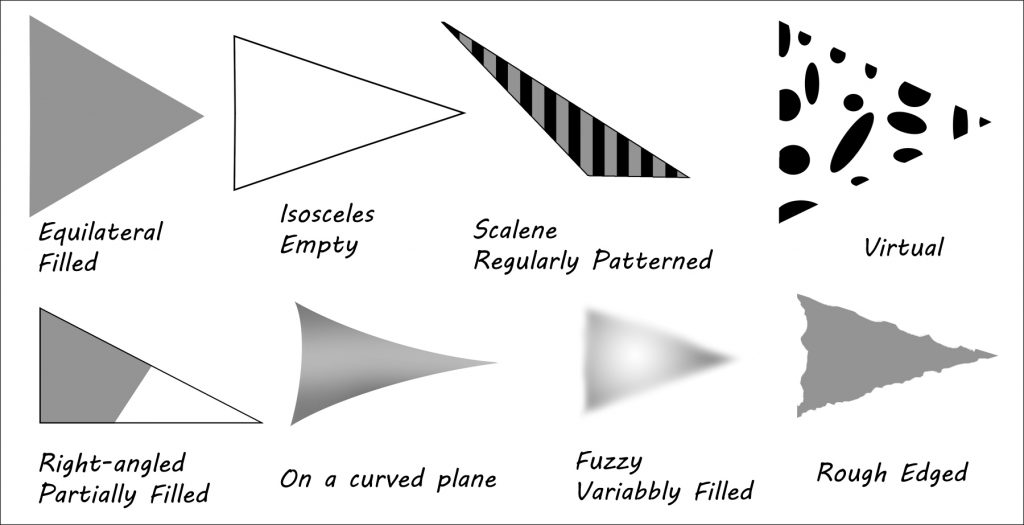
It might be that by seeing the images of equilateral, isosceles, scalene and right angles triangles the novice observer could make or indicate others without ever having a descriptive word or a longer textural definition.
Before reading further, define for yourself the word ‘sheep’. The simplest and perhaps the best way to reach a definition is to point at a sheep and exclaim the word ‘sheep’. This is known as ostensive definition. However the ostensive approach lacks generality in that the particular exemplar might not be characteristic of the range of sheep, for example, that could be observed and pointed at. The example chosen might be a lamb, a ewe or a ram. It might even be a child’s soft toy or a bar of soap moulded into a figurative sheep.

This soap bar reminds us that definition can be expanded by reference. Terms can of course make reference to entities outwith the normal scope of definitions.
If we are to proceed to a lexical definition of sheep that we might encounter in a field the task is considerably more complex. ‘Woolly, quadrupedal, even-toed, ruminant mammals’ is certainly not a substitute for pointing at or exhibiting photographs of sheep. We need to accept the inherent descriptional inadequacy of language. No amount of words conjures into existence the experience of seeing, hearing, smelling, touching interacting with or even eating ‘a sheep’. In other words ‘definitions’ can lack representational completeness. In that sense reliance on ostensive definitions alone would produce a rather meagre way of communicating. In other areas of thought, however, such as mathematics constructivist definitions are central to the emergent complexity of the subject.
c) Operational Definition
There is another kind of definition known as an operational definition. Operational definitions of the number ‘5’ , for example, might be 0+1+1+1+1+1, or 1+4, or 2+3, and so on. Indeed the first example using zero and five ones is the axiomatic basis of our natural number system ( see later section). In this example we are invoking the concept of a logical or arithmetical operation that produces a definition. Similarly, “an even number is an integer number divisible by 2. An odd number is an integer number which is not divisible by 2.”
In the everyday practical world we inhabit, operational definitions are symbolic statements that are the result of a process or human action. A ‘slow walking pace’ might be defined as 2 miles per hour. However to define it only in that way would be to miss the richness and range of meaning that the word ‘slow’ can connote.
At the other end of the velocity range in physics, the ‘speed of light’ can have a precise linguistic definition that relates to the logical concept of calculating speed, where speed is classically defined as the ‘distance travelled’ divided by ‘time’. ‘Light speed’ can be assigned a parametric (or numerical) operational description that is arrived at through the investigations and instrument building by physicists and engineers. The speed (or velocity) of light in a vacuum, c, is defined as 299,792,458 meters per second. If the light then enters a transparent medium, such as water ort glass, the velocity changes and has a different operational definition or measured value.
There are those within the philosophy of science who warn us against ‘operationalism’ or the desire to substitute what should be a theoretical concept for a descriptive measurement. For example the constant ‘c’, or light speed, is also a speed that can be calculated theoretically from Maxwell’s electromagnetic equations. The ‘speed of light in a vacuum’ is a particularly good example of a theoretical concept because it became a theoretical absolute (or mathematical constant) within physical relativity as described by Albert Einstein. With the help of his theory of special relativity, the ‘speed of light’ takes on an even wider theoretical significance and helps us to determine to determine how much energy is in a lump of matter at rest (the energy equivalence of mass) through the elegantly simple and now famous formula E0 = m0c02 ( where E0 is energy, m0 is the mass when at rest with respect to the observer and C0 is the speed of light in a vacuum). There is even the profound philosophical claim that c represents the maximum speed of causality within the universe.
This short video explains, very simply, why the famous equation is a mathematical ‘special case’ that only applies when a mass is at rest relative to the observer. A slightly more complicated equation, E2 = (pc)2 + (mc2)2 where p = momentum is more generally applicable. Some would describe that as ‘relativistic mass’ for the purposes of teaching, however that is not technically precise since the mass is constant and it is the momentum that is increasing. For the context of of the above equation see L.B. Okun (2008) at https://arxiv.org/pdf/hep-ph/0602037.pdf
“Wrong” used by the speaker in the video should not be equated with ‘false’, since it only means that “it is not the whole story” i.e. it is incomplete. The important question to ask yourself is any object ‘truly’ at rest. According to modern cosmology nothing in the universe is at rest so a ‘rest mass’ is an idealised concept.
A final thought
There can be no firm demarcation between what we regard as a definition and what we regard as a description, although the concept of ‘operational definition’ helps to provide a degree of separation. There is instead a rational need for a continuum between definition and description.
Version 1.2
Steve Campbell
Glasgow, Scotland
2019, 2022