2.5.5 Modal and Predicate Logic and Other Topics
Modal Logic Modifies Connections
There are occasions and circumstances in life where we feel certain about some of our explanations and descriptions. There are other situations where the binary properties logical truth and falsity do not provide the expressiveness that we need. The lack of expressiveness can be particular noticeable situations in which we need to qualify our logical conclusions in a way that our ideas are understood within some limiting condition.
Possibility vs. Necessity and Wider Considerations in Modal Logic
You might also be interested in whether a particular line of reasoning is necessarily true or possibly true or could simply be true (in the sense explained by truth tables). These characteristics are referred to as alethic ‘modalities’. ‘Modals’ are simply qualifiers of statements. Possibility is one such modifier. ‘It is not possible for me to go to the local flea market on Saturday to buy antiques because I will be in New York’ uses, the important modifier, possibility. When we admit possibility into logic, we also have logical access to the inverse concept of ‘impossibility’ or ‘not possible’.
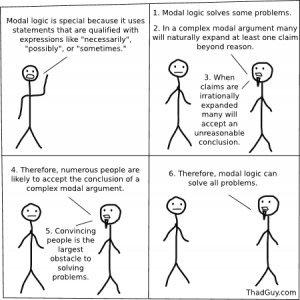
A cartoon from the amazing Thadguy.com entitled ‘Modal Logic Can Solve all Problems’
Another equally important modal is logical necessity. If a statement must be logically true the situation could not be otherwise. In other words, the expression or assertion cannot be false. If you think for less than 10 seconds about situations where logical necessity can be invoked, it becomes immediately obvious that condition only applies when we are dealing with ‘truth by definition’. Water must fall from the sky when it is raining, since that is the definition of rain. Notice however that it is not the only circumstance in which water could fall from the sky. A firefighting aircraft might drop water. Necessity involves at least one circumstance where the condition applies. The same situation applies in integer arithmetic. 1+1 must equal 2. However, 10/5 also equals 2.
Other qualifiers (or modals) can also be invoked. Temporal modals specify the time-dependence of logical values. It might be true that it has been raining in the past. It could be ‘contingently’ true that it might presently be raining. It will rain in the future is the other temporal modifier of the sense in which truth, or a surrogate for truth, that can be applied. However, we do not usually treat future events as knowable in the same way.
Contingency, when describing events or the supposed truth of an assertion, means not necessarily false and not necessarily true. We can see that the contingency of future or present events might not be independently true of what has happened in the past. For example, every year on record it has rained in the West Coast of Scotland, so this seems to create the logical possibility that it could presently be raining. In addition, the previous occurrence of very frequent rain in this location creates the inductive almost certain possibility that it will rain in the future, unless there is a material change in circumstances. Logical modifiers, such as modals or quantifiers, blur still further the practical distinction between deduction in logical systems where a probabilistic outcome is legitimately assertible and inductively supported explanations.
One way to expresses modal qualifiers is to use ‘possible world‘ semantics. For example, we could say that an assertion is possibly true in a possible world. Similarly, true assertions are either presently or historically true in the actual or ‘real’ world in which we live. Naively we might argue that Necessarily true propositions are said to be ‘true in all possible worlds’. If the concept of the world is taken to mean ‘situation’, for example, then some quantifiers of situations might make that interpretation problematic.
Within the field of deductive logic, there have been many systems of logic developed which admit different rules of argument or more than one type of logical implication and make different starting assumptions. In other words, there is not one single formal logic that can be described but instead, there are many that bear different ‘rules of inference’. You might, for example, want to add the notion of ‘relevance‘, which is formally absent in so-called ‘classical’ propositional logic, strange though that may seem. If we admit ‘relevance’ to logic there is a technical need to specify how ‘relevance’ is to be formally understood and devise a formal way of incorporating that into modern symbolical expressions. There is then the additional difficulty in translating the implications of these symbolic statements into ‘natural’ languages, such as English. One strategy for including ‘relevance’ in informal logic has been to modify our understanding of logical implication and to invoke the more fundamental concept of logical necessity to express relevance.
Predicate Logic
Another set of logical modifiers are known as quantifiers used in predicate logic. A proposition or a conclusion used in a logical argument might be modified by the words ‘all’ or ‘every’, ‘none’, ‘each’, ‘some’, ‘many’, ‘most’, and ‘few. It matters a great deal to the sense or meaning of a logical conclusion, for example, if such terms are used because they modify the general applicability of any statement.
For example, the statement ‘Every man in this room is married to a woman in this room does not have the same logical meaning as “Every woman in this room is married”. Indeed both statements can be true if there are more women than men in the room. Equally the statement ‘some women in this room are married’ is logically consistent with the idea of ‘all men the room are married to women in the room’, even if we exclude polygamy.
We can also see from the example of above that these quantities apply within ‘logical domains’ so we can have the domain of ‘all women’ or the domain of ‘all women in the room’ or the ‘domain of all married women in the room’ and so on. These domains, or sets, are alternatively referred to as domains of discourse or ranges over which the quantifiers apply. When the same proposition is applied to different domains its logical implication changes.
The order in which these terms are used and their temporality is also very meaningful. For example, ‘every doctor has been to medical school’ does not have the same logical implication as ‘everyone who has been to medical school is a doctor’ if we include medical school dropouts, retired doctors, and medically qualified people who follow another occupation. In other words, the set (or domain) of ‘all doctors’ and the set of ‘all people who have been to medical school’ are not the same.
Unfortunately, the formal notation of predicate logic is probably quite off-putting for most people. For example, the symbol ‘∀’ is used to represent ‘all’ or more formally ‘for all’ that exists or can be imagined. The idea that something exists is now formally expressed in notation as ‘∃’. The term ∈ is used to mean belongs’ to or ‘is an element of the set of’. An additional complication is that the symbols are combined in particular ways that are specified by the axioms of the logical syntax. There is in effect a formal symbolic language used to express ideas. The relevant Wikipedia article explains the symbolism very clearly using the following example
“Each of Peter’s friends either likes to dance or likes to go to the beach (or both)”, key aspects can be identified and rewritten using symbols including quantifiers. So, let X be the set of all Peter’s friends, P(x) the predicate “x likes to dance”, and Q(x) the predicate “x likes to go to the beach”. Then the above sentence can be written in formal notation as “Each of Peter’s friends either likes to dance or likes to go to the beach (or both)”, key aspects can be identified and rewritten using symbols including quantifiers. So, let X be the set of all Peter’s friends, P(x) the predicate “x likes to dance”, and Q(x) the predicate “x likes to go to the beach”.
Logical Consequence
In a deductive argument when we say it ‘follows that’ a conclusion can be arrived at from the premises, what is it that we are relying on? In formal language, we are asking ‘what is the nature of logical consequence?’ The answer is complex because it depends on whether or not we are dealing with logical possibility (it is possible that a conclusion is sound) or logical necessity (it has to be the case that the conclusion is sound) and whether we are dealing with truth or justification. In addition, any explanation of entailment requires us to decide what rules of logical argumentation (or inference) that we are prepared to accept. In philosophical language, we are asking, what is the basis of deducibility in the context of an agreed system of logic?
In 1936 Alfred Tarski published a brave attempt at an explanation of logical consequence despite the fact that he was aware that ‘We must reconcile ourselves from the start to the fact that every precise definition of this concept will show arbitrary features to a greater or lesser degree’. Tarski tells us 3 conditions must apply in relation to consequence.
First, he insists that we can decide when a consequential relationship exists because we know independently of observational (empirical) evidence. Indeed it would seem pointless to deny that we have the feeling of knowing intuitively when logical consequences apply and when they do not. Whether or not science can advance to a stage where we can go beyond this bold assertion is not at present clear.
Tarski next explains that it is the formal (logical) structure of the arguments that are important and not their content.
Tarski then explains that we also need a ‘modal component’ as part of logical consequence that qualifies the nature of the implied truth relationship. Such a relationship might be: ‘necessary’, ‘contingent’ upon some conditions, as we have already seen, or could be ‘obligatory’ or ‘permissive’. We can then attempt to generalise about the qualifier that is required based on argument types.
If you are starting to feel that there is something incomplete or unsatisfactory about this way of trying to analyse consequence you would not be alone. Tarski was clearly of the view that the ordinary meaning of the word ‘consequence’ was very difficult to encapsulate within a formal logical schema.
Binary Choice
Logical argument has traditionally left the thinker to choose between the dual possibilities of true or false, although there exist other possibilities. You might want to introduce 3 values, rather than use a binary choice. You might, for example, decide to have unknown or unknowable as an additional logical outcome. You might even wish to abandon the idea of binary or multi-valued logical truth and replace that with a continuous range of probabilities, which vary between certain and uncertain (or 0 and 1).
More generally, binary thinking can become an affliction that limits us from seeing other explanatory possibilities.
Informal Logic
It is, of course, possible to construct a formal argument wrongly. These situations can be labelled formal fallacies because they do not correctly apply a particular kind of logic. However, there are erroneous ways of thinking that do not involve formal rules which are known as informal fallacies. The study of common (or informal) fallacies is instructive for it helps us to think more critically. For example, I might say ‘The world will definitely end tomorrow because Fred predicted this was going to happen’. My reasoning would be very weak because I had made a claim of truth based on personal authority rather than on one which seems grounded in a coherent web of explanation and repeated observation. This fallacy of thinking is called ‘an appeal to authority‘. Nevertheless, there are times in life where we all are reliant on personal authority of some form of other. We should, therefore, use our understanding of fallacies carefully and see them more as a heuristic or ‘rule of thumb’. The curious might want to peruse a long list of informal fallacies.
Final Thoughts On Deductive Logic
If deductive structured arguments are to be pragmatically useful, they require truthful statements, helpful descriptions or some other surrogate for truth, such as believability at the outset. When brought together in a particular fashion the premises have the possibility of generating truthful (or useful) statements as their conclusion. Deductive logic does not however independently generate truth, in so far as any statement (or proposition) that is descriptive of the world can ever be said to be ‘true’. It is also worth remembering that all of the implications of ‘logical argument’ are not completely captured by the simple idea of truth or falsity (or binary equivalents) and also requires modifiers, technically known as modals and quantifiers. The idea of logical truth (or a suitable substitute) is a complex idealisation that can be arrived at through various reasoning strategies.
Further Reading
How I Solved Hume’s Problem and Why Nobody Will Believe Me by Eugene Earnshaw, Philosophy Now, Issue 119 2017
https://philosophynow.org/
A Justification of Empirical Thinking by Arnold Zuboff, 2014
https://philosophynow.org/issues/102/A_Justification_of_Empirical_Thinking
Argument
https://en.wikipedia.org/wiki/Argument
Soundness
https://en.wikipedia.org/wiki/Soundness
Deductive and Inductive Arguments by Staff at the Internet Encylopedia of Philosophy
http://www.iep.utm.edu/ded-ind/
There are now long lists of published fallacies
https://en.wikipedia.org/wiki/List_of_fallacies
Logical Consequence by Matthew McKeon, Internet Encylopedia of Philosophy
http://www.iep.utm.edu/logcon/
Modal Logic: A Contemporary View by Johan van Benthem , Internet Encylopedia of Philosophy
http://www.iep.utm.edu/modal-lo/
Logic and Ontology by Thomas Hofweber, The Stanford Encyclopedia of Philosophy (2011)
https://plato.stanford.edu/entries/logic-ontology/
Version 3.2
Steve Campbell
Glasgow, Scotland
2017, 2019, 2022